mathMC “is a 3d function plotter in Minecraft. You can easily plot math functions in your MC world. Minecraft is a 3-dimensional world, so it’s perfect for 3d functions.”
I am happy that mathMC is powered by mXparser 🙂



Best regards,
Mariusz Gromada
Using built-in random variable [Uni] from uniform continuous distribution over [0; 1] interval we sample two numbers (x,y) then check if point is inside the circle. Operation is repeated n-times, then proportion falling into circle is being measured. This is only 1/4 of the circle (positive x and positive y) with radius 1, so 4 times proportion should give estimation of pi.
Argument n = new Argument("n = 100000");
Expression e = new Expression("4 * sum(i, 1, n, if( [Uni]^2 + [Uni]^2 <= 1; 1; 0) ) / n", n);
mXparser.consolePrintln("Res. : " + e.getExpressionString() + " = " + e.calculate());
[mXparser-v.3.0.0] Res. : 4 * sum(i, 1, n, if( [Uni]^2 + [Uni]^2 <= 1; 1; 0) ) / n = 3.14748
Best regards
Dear All,
Recently I found on the internet online calculator powered by mXparser. This is one possible usage scenario of mXparser engine, here only part of functionalities are utilized. (no user defined functions, recursion, only one argument), yet calculator is nice 🙂
Expect mXparser v.3.0.0 release soon 🙂
Best regards,
Mariusz Gromada
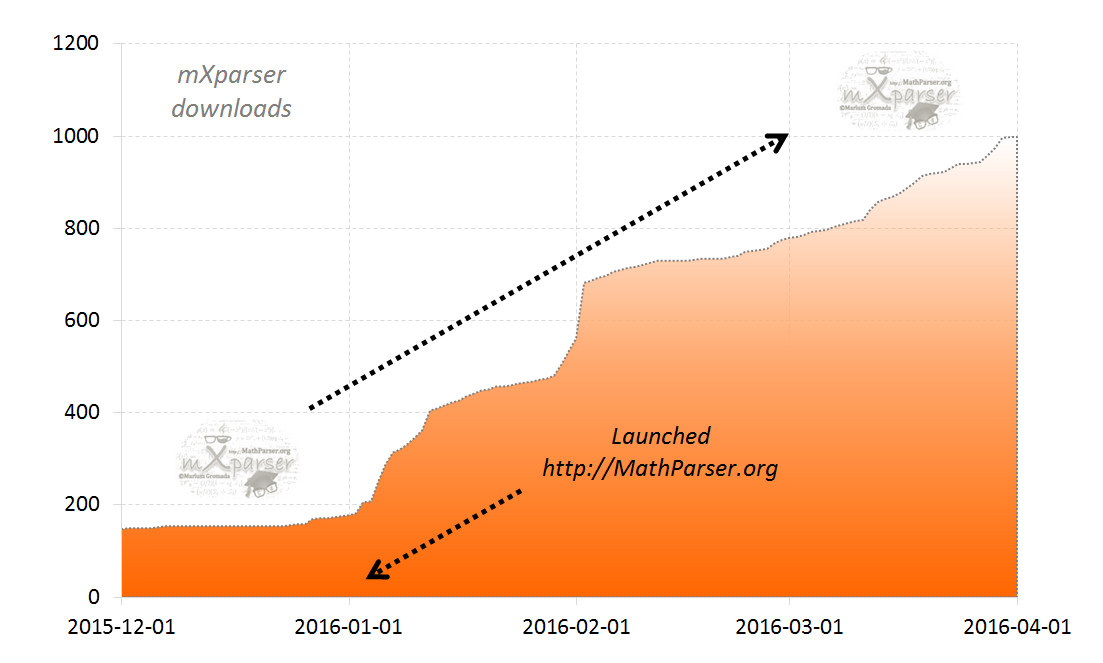
By continuing to use the site, you agree to the use of cookies. more information
The cookie settings on this website are set to "allow cookies" to give you the best browsing experience possible. If you continue to use this website without changing your cookie settings or you click "Accept" below then you are consenting to this.